what annual percent growth rate is equivalent to a continuous percent growth rate of 8

There are two types of exponential growth, and it's easy to mix them upward:

• Discrete growth: change happens at specific intervals
• Continuous growth: change happens at every instant

Here's the deviation:

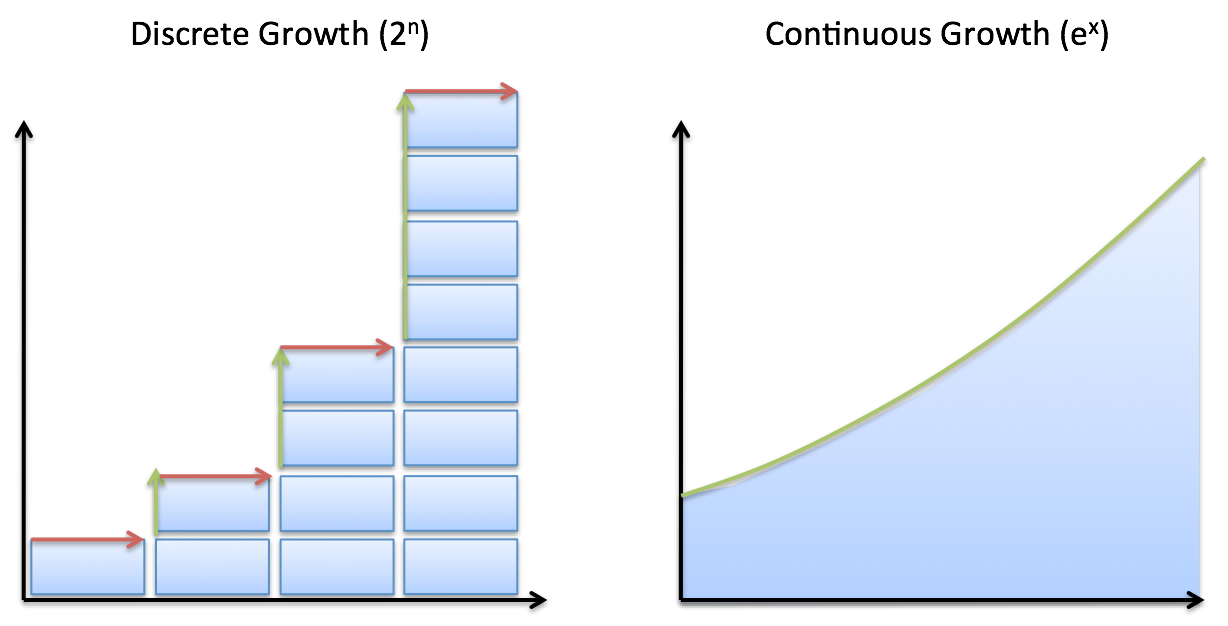
The key question: When does growth happen?

With discrete growth, we can see change happening later a specific event. We flip a coin and get new possibilities. Nosotros have a yearly interest payment. A mating flavor finishes and offspring are built-in.

With continuous growth, change is always happening. We tin can't bespeak to an issue and say "It changed here". The pattern is always in motion (radioactive disuse, a bacteria colony, or perfectly compounded interest).

(Brush up on the number east and the natural logarithm.)

Insight: Convert between discrete and continuous

I visualize change as events along a timeline:

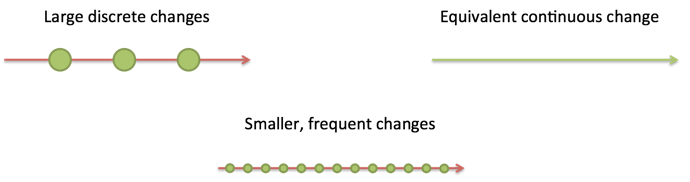
Discrete changes happen as distinct light-green blobs. We tin can take them, separate them into smaller, more frequent changes, and spread them out. With enough splits, nosotros could have smooth, continuous change.

So, discrete changes can exist modeled past some equivalent, shine curve. What does information technology look like?

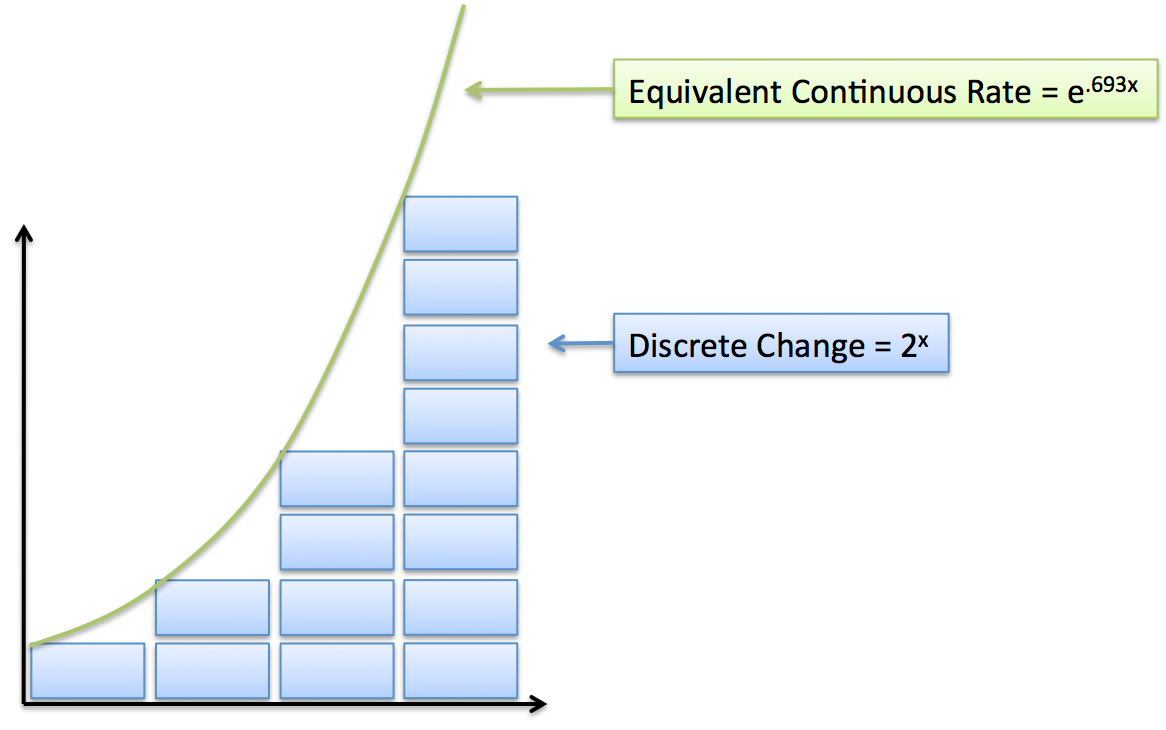
The natural log finds the continuous rate behind a consequence. In our example, we grew from 1 to 2, which means our continuous growth charge per unit was ln(2/1) = .693 = 69.three%. The natural log works on the ratio between the new and old value: $\frac{\text{new}}{\text{old}}$.

Mathematically,

In other words: 100% detached growth (doubling every period) has the aforementioned effect as 69.3% continuous growth. (Continuous growth requires a smaller rate because of compounding.)

So which version do we use?

Now here's the question: how should nosotros talk about growth? It depends on the scenario:

• If growth happens in a man-fabricated system, detached growth works better ($2^ten$, $3^10$)
• If growth occurs a natural system, continuous growth is meliorate ($e^x$)

Let'southward take a look.

Instance: Flipping Coins

Let'due south say nosotros flip a coin. What are the possible outcomes?

• 1 flip: 2 outcomes (H or T)
• 2 flips: 4 outcomes (HH, HT, TH, TT)
• three flips: 8 outcomes (HHH, HHT, HTH, HTT, THH, THT, TTH, TTT)

You see where this is going. I'd describe the number of possibilities as $2^northward$ where n was the number of flips.

I'chiliad using "n" (not x) by convention: 10 could mean any value on the x-axis (-3, 1.234, $\sqrt{14}$), while north represents an integer (1, 2, three, 4).

Could nosotros say the number of outcomes was $e^{\ln(two)x}$, where x was the number of money flips? Yes. Only information technology's confusing: in a human being-made organisation, where nosotros have modify events, I'd utilise the detached version to describe the possibilities.

Example: Binary Numbers

Binary numbers follow the same blueprint: if we take n $.25, we get $2^n$ possibilities. For example, 8 bits have 256 possible values, and xvi bits have 65536.

(At that place may exist some cases where intermediate values make sense, similar representing the number of bits required, even though we need a whole number of $.25 in practice. This is like to saying the average family unit has 2.3 kids.)

Example: Radioactive Decay

When radioactive material decays, we often talk most its half-life: how long until one-half the cloth is gone?

For example, the one-half-life of Carbon-xiv is 5700 years. We could write information technology like this:

If we wait 5700 years, we wait $(one/2)^i= .50$ of the carbon remaining. If we double that and wait 11,400 years, we'd await $(1/2)^ii = .25$ of the carbon left.

However, this equation is written for our convenience. Carbon doesn't decay in jumps, politely waiting around 5700 years and all of a sudden decaying past half. We use (i/two) equally the base of operations because we humans want to count the number of halvings (decomposable into half, decaying into a quarter, decaying into an 8th...).

The radioactive fabric is irresolute every instant. From a physics perspective, a continuous rate is more telling. We can find the continuous decay rate by converting the discrete growth into a continuous pattern:

This helps me sympathise why the natural log is natural -- it'southward describing what nature is doing on an instant-by-instant basis. None of this "wait until we decay past 50% so humans can count it easier" nonsense.

In do, yous don't find the half-life past waiting for carbon to decay fifty%. Y'all'd look a reasonable almost of time (a yr?), use the natural log to find the continuous charge per unit over that period, and work out the half life.

Example: Material X decayed from 53kg to 37kg over 9 months. What's the continuous decay rate and half life (in years)?

The ratio between new and one-time was 37/53, and so ln(37/53) = -.359 = -35.9% continuous growth over our time period. This happened over nine months, so the monthly continuous charge per unit is -35.9/nine = -3.98%. Scaling this up, the yearly continuous rate is -iii.98% * 12 = -47.9%. (Observe how the rate must be scaled to friction match the fourth dimension period. Earning "12% interest" isn't helpful without a time period. "12% interest per twenty-four hour period" is different than "12% interest per year".)

Now that we know the continuous rate is -47.9% per year, we can work out how long until we're at 50%:

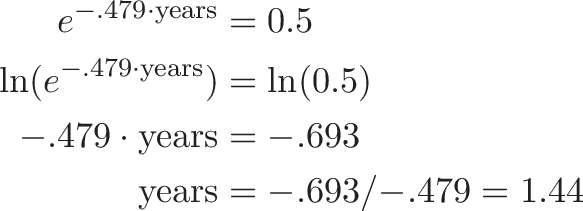
The half-life is 1.44 years.

Example: Stock Market Growth

This is a tricky 1: the stock market place changes every day, so information technology seems like it'd continuous, merely there isn't an underlying predictable rate. We run into a lot of jumpy changes, and sample them at yearly intervals to come across how we're doing. The marketplace is usually described with an annual average growth rate:

A continuous charge per unit of the form $e^x$ doesn't really make sense for the organization. We aren't trying to model our portfolio'south value on a per-instant ground: we desire to know what to await in 30 years.

Example: Population Growth

Population is tricky: depending on the animal, discrete or continuous model can make sense.

A bacteria colony is made of billions of organisms. Although each bacteria cell grows discretely (it has to wait until information technology splits earlier splitting again), the unabridged colony grows smoothly because so many bacteria are in different stages of growth.

Like the radioactive decay example, we can sample the colony at dissimilar time periods and work out how long information technology takes to double. We might accept a continuous rate ($e^x$) that expresses the colony'south instant rate, and a discrete rate ($2^ten$) that helps u.s. humans count the doublings.

1 of my pet peeves were problems like "A bacteria colony doubles after 24 hours...". Argh! Are you telling me the bacteria colony simply happens to have a continuous rate of precisely ln(2) over the course of a day?

I'd prefer you told me the colony doubled while a grad student stared at a petri dish for 24 hours straight. (1.98kg... one.99kg... 2.00kg. I found the doubling time, I tin can go abode! What'southward that Professor? I...ok, I'll work out the continuous rate afterwards an 60 minutes next time.)

Rant aside, how well-nigh modeling a tiger population? Tigers have breeding seasons. They aren't having kids throughout the year, and so the population changes in a discrete event.

(The model gets more complex as you lot account for how long it takes for cubs to have children of their own.)

Onward and Upward

I wrote this post because my video on eastward had questions nigh how $two^x$ represents "staircase growth". Isn't that a smooth curve likewise?

Sure, but nigh of the time we apply 2 as a base to model discrete patterns. $2^n$ (where n is an integer) models discrete scenarios similar coin flips or binary digits. If your system does change continuously, why not provide the continuous rate and write $e^{\ln(2) ten}$?

In that location's no right and wrong here, just the bulletin we convey. A whole-number base ($two^10$, $3^x$) implies you lot desire people to recall about whole-number values of x (and half-life is a good case). Using $e$ as a base ($eastward^{\text{charge per unit} \cdot \text{time}}$) implies you lot want people to think about change that happens at every moment.

Either way, be fluent in both models and learn to hop betwixt the two.

Happy math.

Other Posts In This Series

1. An Intuitive Guide To Exponential Functions & e
2. Demystifying the Natural Logarithm (ln)
3. A Visual Guide to Simple, Compound and Continuous Interest Rates
4. Common Definitions of eastward (Colorized)
5. Understanding Exponents (Why does 0^0 = 1?)
6. Using Logarithms in the Existent World
7. How To Call back With Exponents And Logarithms
8. Agreement Discrete vs. Continuous Growth
9. What does an exponent really mean?
10. Q: Why is eastward special? (two.718..., not ii, 3.7 or another number?)

millerpentat.blogspot.com

Source: https://betterexplained.com/articles/understanding-discrete-vs-continuous-growth/

Share this post